Gibbs Sampler Colapsado

Para isso, as seguintes atividades foram desenvolvidas a partir de bases reais de documentos:

• Implementação do modelo LDA ( Gibbs Sampler padrão);
• Implementação do algoritmo Collapsed Gibbs Sampler conforme descrito no artigo de Griffiths and Steyvers (2004).

• Modelar documentos oriundos de múltiplos tópicos;
• Um tópico é definido como tendo uma distribuição de probabilidade sobre um vocabulário fixo de palavras;
• Assume-se que K tópicos estão associados a uma coleção de documentos; e
• Cada documento exibe os tópicos com diferentes proporções.

Mais formalmente, o LDA se baseia em :

• um modelo de variáveis latentes para os documentos;
• os dados observados são as palavras de cada documento;
• a estrutura de tópicos é uma estrutura latente. Dado uma coleção, a ditribuição a posteriori das variáveis latentes determina a decomposição de tópicos da coleção.

A interação entre os documentos observados e a estrutura de tópicos latente se manifesta em um processo probabilístico gerador associado ao LDA, processo aleatório imaginário que se assume ter produzido os dados observados.

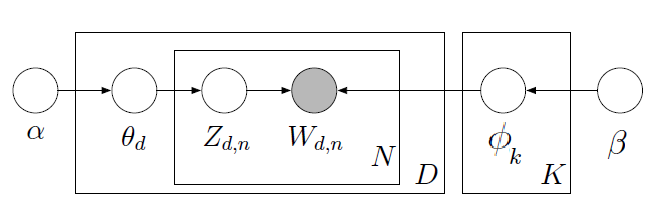
Figura 1 : Modelo LDA

• \(\alpha\) e \(\beta\) = hiperparâmetros conhecidos a priori;
• \(\theta_d \sim Dir(\alpha)\) = proporção de tópicos por documento
• \(\phi_k \sim Dir(\beta)\) = K vetores M-dimensionais com dist. probabilidade sobre as M palavras do dicionário.
• \(z_{d,n} \sim Mult(1,\theta_d)\) = atribuição de cada palavra a um tópico
• \(w_{d,n} | z_{d,n} \sim Mult(1,\phi_{z_{d,n}})\) = palavra observada

O processo pode ser descrito como :

• Documento escolhe seus tópicos \(\theta_d = (\theta_{d1}, \theta_{d2}, \theta_{d3}, ..., \theta_{dk})\) que são vetores i.i.d com distribuição Dir(\(\alpha_1,\alpha_2,\alpha_2,...,\alpha_k\)) ;
• Seleciona palavras do dicionário \(1,2,...,M\), onde cada palavra do documento \(d\) seleciona seu tópico \(z_{dn}\).
• \(z_{dn}\) é uma variável aleatória discreta com valores \(1,2,3,...,k\) e probabilidades associadas \(\theta_d = (\theta_{d1}, \theta_{d2}, \theta_{d3}, ..., \theta_{dk})\);
• \(z_{dn}\) é o tópico de onde a palavra \(n\) do documento \(d\) vai ser escolhida.
• \(z_{dn}\) são i.i.d com distribuição \(Mult(1;\theta_d\));
• Dado o tópico \(z_{dn}\), a \(n\)-ésima palavra do documento \(d\) é escolhida do dicionário \(1,2,...,M\) com probabilidades dados por \(\beta_{z_{dn}}\), vetor associado ao seu tópico.

O vetor de parâmetros pode ser assim visualizado :

Figura 1 : Modelo LDA

A partir do gráfico acima obtemos a distribuição conjunta dos dados e das variáveis, a saber :

• \(n_{k,m}\) = número de vezes que o tópico \(k\) e a palavra \(m\) foram escolhidos.
• \(n_{d,k}\) = número de palavras do documento \(d\) que pertencem ao tópico \(k\).
• \(X\) = matriz de dimensão D × N onde \(X[d, n]\) é o índice da \(n\)-ésima palavra no documento \(d\). Isto é, \(x[d, n] = m\) significa que a \(n\)-ésima palavra do documento \(d\) foi a palavra \(m\) do dicionário.

• \(X[d, n]\) = valores coletados nos documentos.

A seguir apresentamos o altoritmo Gibbs Sampler Padrão:

Inicialização : \(\theta^{(0)}\), \(\phi^{(0)}\), \(z^{(0)}\), \(\alpha\), \(\beta\); sendo \(\theta\) e \(\phi\) Dirichlet simétrica

Para cada iteração \(i\) faça :

Para cada tópico \(k\) calcule \(n_{k,m}\)

Simule \(\phi\) a partir de uma dirichlet com parâmetros (\(n_{k,m}\) + \(\beta\))

Para cada documento \(d\) faça :

Para cada tópico \(k\) calcule \(n_{d,k}\)

Simule \(\theta\) a partir de uma dirichlet com parâmetros (\(n_{d,k}\) e \(\alpha\))

Para cada palavra \(n\) Simule \(z_{d,n}\) a partir de \(\theta\) e \(\phi\)

Fim para

Fim para

Antes de apresentarmos o algoritmo collapsed Gibbs Sampler (CGS) vamos detalhar a distribuição de probabilidade para a qual o algoritmo gera amostras.

O algoritmo CGS calcula a distribuição de probabildade de um tópico \(z\) atribuído a uma palavra \(m\), dado todas as palavras e todos os demais tópicos atribuídos a todas as outras palavras.

Formalmente estamos interessados em calcular a seguinte distribuição a posteriori, a menos de uma constante : \[p(z_i | \mathbf{z_{-i}},\textbf{w},\alpha, \beta)\]

O algoritmo CGS calcula a probabilidade acima a partir do cálculo da distribuição marginal conjunta de (z,w), através da integração da distribuição conjunta de todos os dados e variáveis, \(p(\textbf{z},\textbf{w},\theta,\phi | \alpha,\beta)\), sobre as variáveis \(\theta\) e \(\phi\), ou seja :

Assim, pela regra de Bayes, temos que \(p(\textbf{z} | \textbf{w}, \alpha,\beta) \propto p(\textbf{z},\textbf{w} | \alpha,\beta)\), e a partir das regras de probabilidade condicional, temos :

onde \(\mathbf{z_{-i}}\) significa todas as atribuições de tópicos efetuadas às palavras, exceto para \({z_i}\).

Seguindo o modelo LDA onde

\[p(\textbf{z},\textbf{w},\theta,\phi | \alpha,\beta) = p(\textbf{z} | \theta) p(\textbf{w} |\phi_z)p(\phi | \beta) p(\theta | \alpha) \]

podemos expandir a equação (1) e obter :

Agrupando os termos que têm variáveis dependentes, obtemos :

Observamos que as duas integrais são distribuições de probabilidade compostas de distribuições multinomiais com distribuições dirichlet, resultando no produto de duas distribuições .

Começando com o primeiro termo, temos :

\[ \int p(\textbf{z} | \theta)p(\theta | \alpha)d\theta = \int \prod_d \prod_i \theta_{d,z_i} \frac{1}{\beta(\mathbf{\alpha})} \prod_k \theta_{d,k}^{\alpha_k - 1}d\theta_d\]

onde \(\alpha = (\alpha_1,..., \alpha_k)\), \(B(\alpha)\) é a função beta multinomial, e \(n_{d,k}\) = número de vezes que palavras do documento \(d\) foram atribuídas ao tópico \(k\).

Para o segundo termo, temos :

\[ \int p(\textbf{w} |\phi_z)p(\phi | \beta) d\phi = \int \prod_d \prod_i \phi_{z_{d,i},w_{d,i}} \prod_k \frac{1}{B(\beta)} \prod_w \phi_{k,w}^{\beta_w - 1}d\phi_k\]

onde \(\beta = (\beta_1,..., \beta_k)\), e \(n_{k,w}\) = número de vezes que a palavra \(w\) foi atribuída ao tópico \(k\).

Combinando as equações (5) e (6), a distribuição conjunta \((\textbf{z}, \textbf{w})\) é dada por:

Retornando à equação (2) (mas sem os hiperparâmetros \(\alpha\) e \(\beta\) para simplificar), temos :

\[p(z_i = k | \mathbf{z_{-i}},\textbf{w}) = \frac{p(\mathbf{z},\textbf{w})}{p(\mathbf{z_{-i}},\textbf{w})} \propto \frac{B([n_{d,k}]_{k=1}^K + \alpha)}{B([n_{(d,k)}^{(-i)}]_{k=1}^K + \alpha)} \frac{B([n_{k,w}]_{w=1}^W + \beta)}{B([n_{(k,w)}^{(-i)}]_{w=1}^W + \beta)} \]

\[p(z_i = k | \mathbf{z_{-i}},\textbf{w}) \propto \frac{\Gamma(n_{d,k} + \alpha_k)\Gamma(\sum_{k=1}^K n_{(d,k)}^{(-i)} + \alpha_k)}{\Gamma(n_{(d,k)}^{(-i)} + \alpha_k)\Gamma(\sum_{k=1}^K n_{d,k} + \alpha_k)} \frac{\Gamma(n_{k,w} + \beta_w)\Gamma(\sum_{w=1}^W n_{(k,w)}^{(-i)} + \beta_w)}{\Gamma(n_{(k,w)}^{(-i)} + \beta_w) \Gamma(\sum_{w=1}^W n_{k,w} + \beta_w)} \]

Uma vez apresentado a distribuição de probabilidades para a qual o algoritmo CGS irá gerar amostras e considerando que os hiperparâmetros \(\alpha\) e \(\beta\) são atribuídos um único valor (dirichlet simétrica), segue abaixo o algoritmo para gerar essas amostras :

Entrada : palavras w \(\in\) documentos d

Saída : tópicos z e contadores \(n_{d,k}\), \(n_{k,m}\), \(n_k\), e \(n_d\)

Início

Inicialize aleatoriamente z e incrementa contadores

Para cada documento \(d\) faça:

Para \(i = 0\) até \(N\) - 1 faça:

\(palavra\) = \(w[i]\)

\(topico\) = \(z[i]\)

\(n_{d,topico}\) -= 1

\(n_{topico,palavra}\) -= 1

\(n_{topico}\) -= 1

Para \(k = 0\) até \(K\) - 1 faça:

\(p(z = k | .)\) = \(\frac{n_{d,k} + \alpha_k}{n_d + K \alpha} \frac{n_{k,w} + \beta_w}{n_k + W \beta}\)

Fim Para

\(topico\) = sample de \(p(z | .)\)

\(z[i]\) = \(topico\)

\(n_{d,topico}\) += 1

\(n_{topico,palavra}\) += 1

\(n_{topico}\) += 1

Fim Para

Fim Para

retorne z,\(n_{d,k}, n_{k,w}, n_k, n_d\)

Fim

Como as distribuições a posteriori de \(\theta\) e \(\phi\) são distribuições dirichlet

\[(\theta_d | .) \sim Dir(n_{d,1} + \alpha_1, ..., n_{d,k} + \alpha_k)\] \[(\phi_w | .) \sim Dir(n_{k,1} + \beta_1, ..., n_{k,w} + \beta_k)\]

para termos uma estimativa dessas variáveis, basta calcularmos o valor esperado de cada um conforme abaixo :

\[\hat{\phi}_{k,w} = \frac{n_{k,w} + \beta_k}{n_k + W \beta } \] \[\hat{\theta}_{d,k} = \frac{n_{d,k} +\alpha_k}{n_d + K \alpha } \]

A seguinte coleção de documentos foi utilizada :

• Journal of Statistical Software (JSS) até 08/05/2010 utilizada no artigo topicmodels: An R Package for Fitting Topic Models .

Nesse item apresentaremos a comparação entre os resultados das implementações :

• Implementação própria do Gibbs Sampler Padrão;
• Implementação própria do Collapsed Gibbs Sampler